목차
1. 선택 정렬(selection sort)
2. 삽입 정렬(insertion sort)
3. 버블 정렬(bubble sort)
4. 합병 정렬(merge sort)
5. 셸 정렬(shell sort)
6. 퀵 정렬(quick sort)
7. 힙 정렬(heap sort)
8. 위상 정렬(topological sort)
1. 선택 정렬(selection sort)
자리를 하나 선택하고, 데이터 중 최솟값을 찾아서, 선택한 자리의 데이터와 교환을 반복해 정렬하는 알고리듬입니다.
1) 첫 번째 자리를 선택하고, 나머지 데이터 중 최솟값을 찾아서 자리를 교환
2) 두 번째 자리를 선택하고, 나머지 데이터 중 최솟값을 찾아서 자리를 교환
3) 위를 반복해 정렬을 완료

구현이 비교적 단순하지만, 시간 복잡도는 O(n^2)으로 비효율적인 편입니다.
2. 삽입 정렬(insertion sort)
데이터를 하나씩 순회하면서, 그 데이터에 맞는 위치를 찾아 삽입하는 방식의 정렬 알고리듬입니다.
1) 두 번째 데이터를 왼쪽 데이터들과 모두 비교해서 데이터 교환을 통해 삽입
3) 세 번째 데이터를 왼쪽에 적절한 위치로 삽입
3) 위를 반복해 정렬을 완료

선택 정렬과 마찬가지로, 구현이 비교적 단순하지만, 시간 복잡도는 O(n^2)으로 비효율적인 편입니다.
3. 버블 정렬(bubble sort)
인접한 두 데이터를 비교해서 교환을 반복하고, 교환할 게 없으면 정렬을 완료하는 정렬 알고리듬입니다.
1) 인접한 두 데이터를 비교 후 교환을 반복
2) 교환이 없을 때까지 반복해 정렬을 완료

삽입/선택 정렬과 마찬가지로, 구현이 비교적 단순하지만, 시간 복잡도는 O(n^2)으로 비효율적인 편입니다.
4. 합병 정렬(merge sort)
폰 노이만이 고안한 방법으로, 분할 정복 방식을 사용하는 알고리듬입니다.
데이터들을 균등하게 두 개로 나누고, 각각 정렬을 완료한 후에 점진적으로 합병해서 정렬을 완료합니다.
1) 더 이상 나눌 수 없을 때까지 데이터를 두 영역으로 나눔
2) 나눈 데이터들을 점진적으로 정렬하고 합병해서 전체 정렬을 완료

구현이 비교적 어렵지만, 시간복잡도는 O(N * logN)으로 빠른 편입니다.
5. 쉘 정렬(shell sort)
데이터가 어느 정도 정렬이 되어 있을 때 ,삽입 정렬의 성능이 좋다는 것에서 고안된 방법입니다.
특정 간격(Gap)으로 데이터를 나누어 미리 정렬을 해놓은 뒤, 삽입 정렬을 사용해 정렬을 완료하는 알고리듬입니다.
1) Gap을 미리 설정
2) Gap으로 나뉘어진 데이터들(쉘) 중, 서로 같은 위치에 있는 데이터를 비교해 위치를 교환
3) 쉘 들의 데이터를 모두 비교했다면, Gap을 1/2로 설정 후 다시 비교
4) 위 과정을 Gap이 1이 될 때까지 수행
5) 마지막엔 삽입 정렬로 최종 정렬을 완료

구현이 비교적 쉽고, 평균 O(n^1.5), 최악 O(n^2)의 시간복잡도를 가지는 비교적 빠른 정렬 알고리듬입니다.
6. 퀵 정렬(quick sort)
Pivot을 정한 뒤, start, end 지점을 이동시켜 Pivot보다 작은 데이터는 왼쪽으로, 큰 데이터는 오른쪽으로 파티셔닝해서 재귀적으로 처리하는 정렬 알고리듬입니다.
1) 가장 왼쪽 또는 오른쪽의 데이터를 Pivot으로 설정합니다.
2) start의 인덱스를 이동시켜 Pivot 값보다 큰 값을 찾습니다.
3) end의 인덱스를 이동시켜 Pivot 값보다 작은 값을 찾습니다.
4) start와 end의 데이터를 서로 교환합니다.
5) 위 과정을 반복해서 start와 end의 인덱스가 엇갈리면 탐색을 종료하고, Pivot 데이터를 교환합니다.
6) 이제 왼쪽엔 이전 Pivot 보다 작은 값으로, 오른쪽엔 큰 값으로 파티셔닝됩니다.
7) 각 파티션에서 다시 Pivot을 정하고, 위 과정을 반복해 정렬을 완료합니다.

구현이 비교적 어렵지만, 평균 O(N * logN) 최악 O(N^2)의 시간복잡도를 갖는 빠른 속도의 정렬 알고리듬입니다.
7. 힙 정렬(heap sort)
자료구조 중 하나인 힙 트리의 최대값과 최솟값을 빠르게 구할 수 있다는 점을 활용한 정렬 알고리듬입니다.
정렬 과정을 알기 위해선, 힙 트리의 삽입과 삭제 과정을 이해해야 합니다.
https://sty110357.tistory.com/31
1) 데이터의 왼쪽부터 하나씩 힙 트리에 삽입
2) 힙 트리가 구성되면, 최솟값 또는 최댓값을 힙 트리에서 삭제 과정을 거쳐 정렬을 완료

O(N * logN)의 시간복잡도를 가지기 때문에 퀵, 합병 정렬과 같이 빠른 정렬 알고리듬에 속합니다.
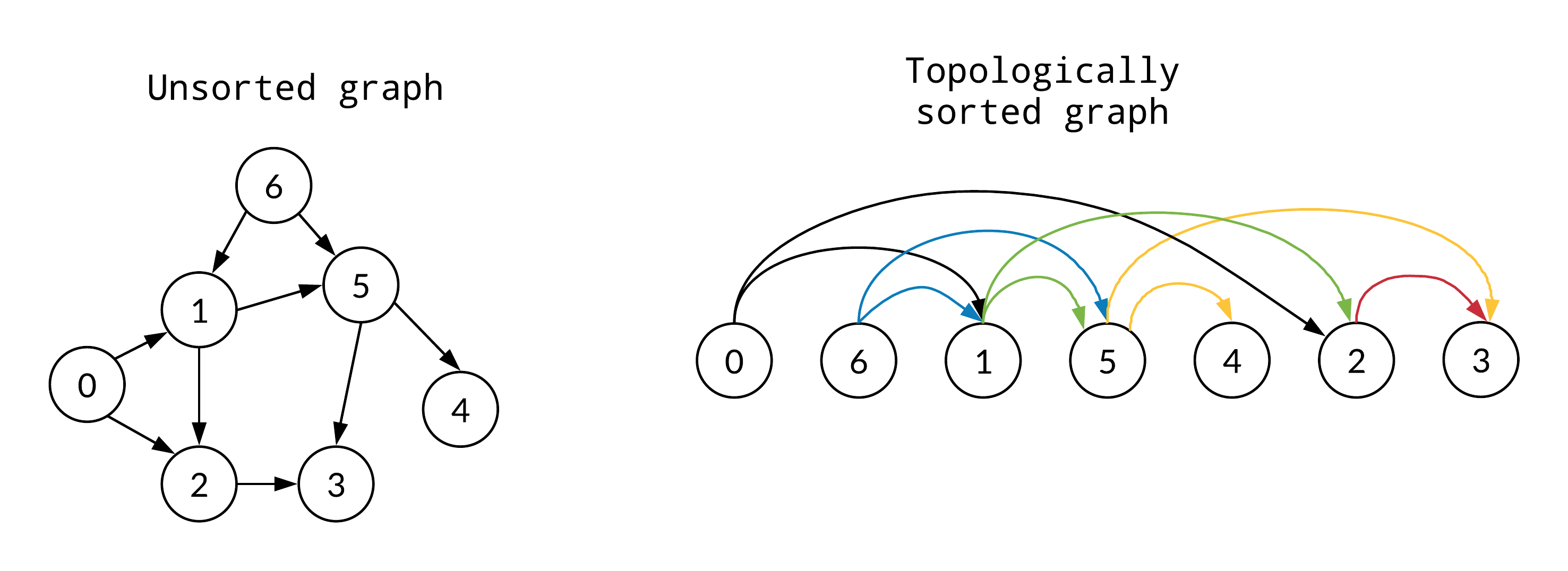
8. 위상 정렬(topological sort)
사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 정렬 알고리듬입니다.
즉 순서가 정해져 있는 작업을 어느 순서로 수행해야 하는지 결정하기 위해 사용되는 알고리듬입니다.
* 진입차수 : 한 노드로 진입하는 간선의 수
* 진출차수 : 한 노드에서 다른 노드로 진출하는 간선의 수
1) 진입차수가 0인 노드들을 큐에 넣고, 이 노드들의 진출 차선을 그래프에서 제거
2) 새롭게 진입차수가 0이 된 노드들을 큐에 넣고 진출 차선을 그래프에서 제거
3) 위 과정을 반복해 정렬을 완료
* 정렬 알고리듬 속도 비교
| Name | Best | Average | Worst | Run-time(60,000개, sec) |
| 삽입 정렬 | n | n^2 | n^2 | 7.438 |
| 선택 정렬 | n^2 | n^2 | n^2 | 10.842 |
| 버블 정렬 | n^2 | n^2 | n^2 | 22.894 |
| 쉘 정렬 | n | n^1.5 | n^2 | 0.056 |
| 퀵 정렬 | n log n | n log n | n^2 | 0.014 |
| 힙 정렬 | n log n | n log n | n log n | 0.034 |
| 합병정렬 | n log n | n log n | n log n | 0.026 |
이 글은 아래 링크의 글을 참고해 작성했습니다.
https://gmlwjd9405.github.io/2017/10/01/basic-concepts-of-development-algorithm.html
'Fundamental > Algorithm' 카테고리의 다른 글
| [JavaScript] 요세푸스 순열 문제 (0) | 2021.11.30 |
|---|---|
| 다익스트라(Dijkstra's) 알고리듬 간략 정리 (0) | 2021.11.21 |
| 최소 비용 신장 트리 알고리즘 간략 정리 (0) | 2021.11.21 |
| 그래프 탐색 알고리듬 간략 정리 (1) | 2021.11.21 |
| 자료구조 간략 정리 (1) | 2021.11.19 |



