
알아야 하는 이유
예를 들어, 인공지능 모델이 사람의 키, 몸무게, 온도 같은 연속적인 수치 데이터를 예측하거나 분류할 때가 많다.
이런 경우 예측값이나 실제 데이터가 딱 떨어지는 정수나 이산값이 아니라, 실수 값으로 나타나므로,
이산확률분포 대신 연속확률분포를 이해하고 활용해야 한다.
이산확률분포가 “성공/실패 같은 명확한 결과의 횟수”를 다룬다면,
연속확률분포는 “측정값이나 예측값처럼 실수 범위에 있는 값들의 분포와 불확실성”을 이해하고 다루는 데 필수적이다.
따라서 딥러닝에서 데이터 특성에 맞는 확률분포를 선택하고 활용하려면 연속확률분포에 대한 이해가 꼭 필요하다.
⭐️ 연속 확률 분포(Contrinuous Probability Distribution)
- 확률 변수 X가 취할 수 있는 값이 무한한 경우에 사용됨
- 이때 연속 확률 분포는 연속 확률 변수의 확률 분포를 의미한다.
- 특정한 값 x에 대한 정확한 확률 값을 표현할 수 없으므로, 특정한 구간 a <= x <= b에 대한 확률(면적)로 표현한다.
- 확률 변수 X가 어떠한 구간에 속할 확률은 0과 1 사이이며, 모든 구간의 확률을 합치면 1이다.
- 이를 확률 밀도 함수(PDF, Probability Density Function)으로 표현하면 아래와 같다.

- 즉, a부터 b까지의 구간에 대하여 "확률 x 구간 길이"의 값을 모두 더한 값이다.
균등 분포(Uniform Distribution)
- 특정 구간 내 값들이 나타날 확률이 균등하다.
- 즉, 모든 확률 변수 X에 대해 일정한 확률을 가지는 확률 분포이다.
- X가 균등 분포를 따를 때 X ~ U(a, b)로 표현한다.

예시
- 확률 변수 X가 구간 [10, 20]에서 균등한 분포를 가질 때, P(15 <= X <= 17)은?
- X ~ U(10, 20) = f(x) = 1 / (20 - 10)
- f(x) * dx = 1/10 * (17 - 15) = 1/5
⭐️ 정규 분포(Normal Distribution), 가우스 분포(Gaussian Distribution)
- 평균 주변으로 값이 가장 많이 모이고, 좌우로 갈수록 값이 점점 희박해지는 대칭적인 분포
- 정규 분포의 모양은 평균과 표준편차로 결정된다.
- 관측되는 값의 약 98%가 ±2σ 범위 안에 속한다.(σ = 표준편차)

정규 분포의 확률밀도함수(PDF)
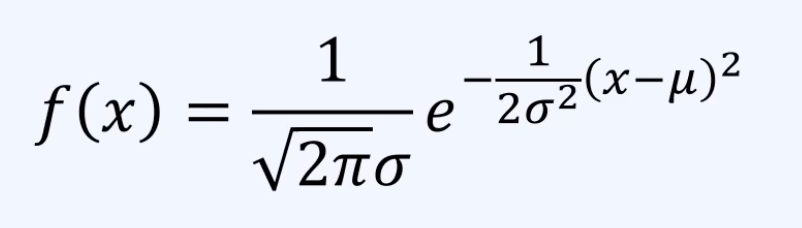

- PDF는 어떤 값 근처에서 값이 나올 "가능성의 밀도"를 나타낸다.
- 값이 높다 = 그 근처 값이 자주 나온다.
- 값이 낮다 = 그 근처 값이 드물게 나온다.
- 예를 들어, 평균이 70점인 시험에서
- 70점 근처가 가장 많음(높은 PDF 값)
- 100점은 상대적으로 적음(낮은 PDF 값)
- PDF 값 자체는 확률이 아니고, 면적(적분값)이 확률이 된다.
지수 분포(Exponential Distribution)
- 특정 시점에서 어떤 사건이 일어날 때까지 걸리는 시간을 측정할 때 사용한다.
- 포아송 분포는 사건의 "발생 횟수"에 대한 확률을 구할 때 사용되며,
- 지수 분포는 어떤 사건이 랜덤하게 발생할 때, 다음 사건까지 기다리는 "시간"을 구할 때 사용된다.
- 예시) 운영 중인 서버에는 하루 평균 4건의 해킹이 시도된다. 이때 첫 번째 해킹 시도가 3시간 안에 발생할 확률은?
⭐️ 표준 정규 분포(Standard Normal Distribution)
- 평균(µ)이 0, 표준편차(σ)가 1인 표준화된 정규 분포를 의미한다.
- 확률을 계산하기 위해 정규 분포 함수를 직접 적분하는 것은 매우 어렵고 번거롭다.
- 그래서 정규 분포 함수를 표준 정규 분포로 변환한 뒤에 확률을 계산한다.

- 예를 들어 P(Z <= 1) 확률은 약 84.1%로 볼 수 있다.
- 표준 정규 분포는 0을 기준으로 좌우 50% 대칭되므로 50 + 34.1 = 84.1이다.
특히 표준 정규 분포를 사용하면 각 구간에 대한 확률을 미리 계산해놓은 표준 정규 분포 표가 있기 때문에,
확률을 새로 계산할 필요가 없이 바로 대입해서 계산할 수 있기 때문에 매우 편리하다.

예를 들어, 표준 정규 분포에서 P(0 <= Z <= 0.75)가 얼마인지 구한다면 표를 기준으로 0.7734 - 0.5 = 0.2734로 쉽게 구할 수 있다.
확률 변수 X가 X ~ N(µ, σ^2)를 따를 때, 다음의 공식으로 표준화할 수 있다.

- 흔히 지능 지수(IQ)를 판단할 때, 평균 IQ를 100으로 설정한다.
- 한국에서는 기본적으로 표준 편차 σ를 24로 설정한다.
- IQ가 148이라면, 상위 몇 %에 해당할까?
- X ~ N(100, 24^2)일 때, X가 148 이상일 확률
- P(X >= 148) = (148 - 100) / 24 = 2
- P(Z >= 2) = 1 - 0.9713 = 0.0287 => 상위 2.87%
딥러닝에서는 이를 활용하여 입력 데이터를 N(0, 1) 분포를 따르도록 표준화하여 학습하는 경우가 많다.

이처럼 확률 분포를 알면 새 데이터가 평균/일반적인지 측정할 수 있으며,
기존 데이터에서 확률 분포 상 높은 확률을 가지는 부분에 위치한 데이터를 샘플링하기 수월하다.
'ML > Statistics' 카테고리의 다른 글
| [ML] Statistics - 기술 통계: 요약 지표 (1) | 2025.06.08 |
|---|---|
| [ML] Statistics - ⭐️ 확률 변수 간 관계 (1) | 2025.06.07 |
| [ML] Statistics - 이산 확률 분포 (0) | 2025.05.31 |
| [ML] Statistics - 확률 기초 (1) | 2025.05.31 |



